2x2 Matrix
Let’s review how to calculate determinant of a 2x2 matrix. For example, given below matrix:
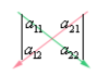
\[ det(A) = a11a12-a12a21 \]
from the image, we can conclude that it equals to GREEN arrow minus RED arrow.
3x3 Matrix
Let’s move to 3x3 matrix, given below matrix:
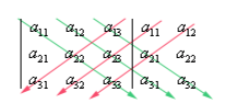
\[ det(A) = a11a22a33 + a12a23a31 + a13a21a32 - a12a21a33 - a11a23a32 - a13a22a31 \]
again, from the image, we can conclude that it equals to GREEN arrow minus RED arrow, except that in this time, we write the first column and second column one more time.
As far as I know, the trick is just working in this 2 situations.
nxn triangular matrix
the matrix is with diagonal entries \( a11, a22, …, ann \), then
\[ det(A) = a11a22…ann \]
nxn matrix
minor and cofactor of \(a_{ij}\)
minor of \(a_{ij}\)
If A is a square matrix then the minor of \(a_{ij}\),
denoted by \(M_{ij}\),
is the determinant of the submatrix that results from removing the \(i^{th}\) row and \(j^{th}\) column of A.
cofactor of \(a_{ij}\)
If A is a square matrix then the cofactor of \(a_{ij}\),
denoted by \(C_{ij}\),
is the number \( (−1)^{i+j} M_{ij} \).
two ways to calculate
- Choose any row, say row i, then,
\[ det(A) = a_i1Ci1 + ai2Ci2 + … + ainCin \]
- Choose any column, say column j, then,
\[ det(A) = a1jC1j + a2jCwj + … + anjCnj \]